遗忘的数学知识
1.欧拉公式
欧拉公式的证明可以用幂级数展开式来证明,如下:

2.二维向量与复数的对应关系
定义
设二维向量:
我们可以把它写成一个复数:
实部 x 对应向量的 x 方向
虚部 y 对应向量的y方向
这样,每个二维向量就对应复平面上的一个点,或者说是一个复数。
优势
1.加法对应向量加法:
若:v1=(x1,y1),v2=(x2,y2),对应复数:z1=x1+iy1,z2=x2+iy2
复数加法:z1+z2=(x1+x2)+i(y1+y2)
恰好等于向量加法v1+v2
2.旋转对应乘以
二维向量旋转θ弧度:
写成复数形式为:
这样旋转就变成了复数乘法,非常方便。
3.模长对应向量长度:
3.旋转公式推导
二维矩阵逆时针旋转θ 的公式为:
推导过程如下:
设二维向量:
在平面旋转θ 弧度得到v′=(x′,y′)。
如果把v写成极坐标的形式:
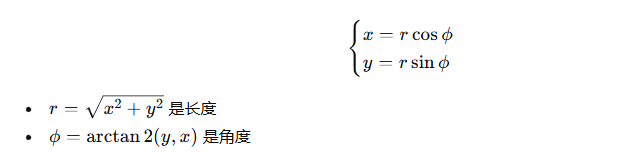
旋转 θ 后:
利用三角函数加法公式
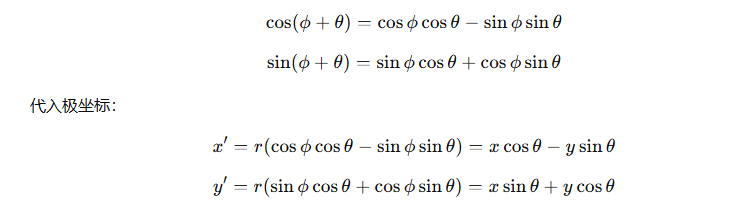
把旋转公式写成矩阵形式为:
4.二维向量做内积
给两个二维向量,它们的内积定义为:
几何意义为投影×长度:
如果把 向量 a 沿着向量 b 的方向投影,则它的大小就是a在b方向上的影子:
再乘上b的长度:
这可以表示a在b方向上有多少成分×b的强度
内积越大,则表示两个向量越相似:
在self_attention的计算当中,则可以表示Query与Key的对齐程度。
5.三角函数的性质
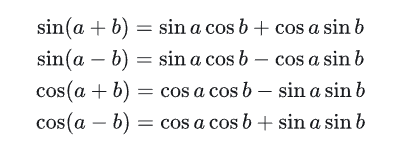
6.内积与外积的概念
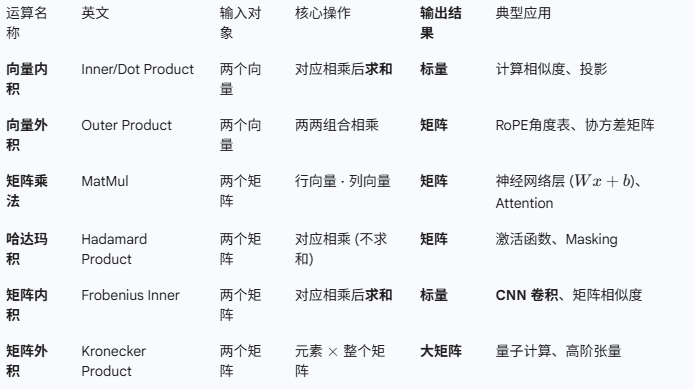
7.牛顿迭代法
从几何角度来看,是在xn处,对曲线求切线,以这个切线方向下降,总能下降到逼近0点的位置。所以这条切线是y=kx+b,经过(xn,f(xn)),k=f'(xn),即可求出切线,另切线的y=0,即可求出一次迭代后更新的坐标xi。xi总比上一次小(从曲线右侧凸函数开始迭代)。
从数学角度来看,即在xn处把函数做一阶泰勒展开:
我们要求f(x)=0,则迭代公式为: