Skip to main content

Fp32以及BF16与FP16分析

image-20251212204215116

数值范围推导​

正确公式来自 IEEE 754 浮点数格式，指数是 以 2 为底数的偏移二进制指数（biased exponent)，不是以 10 为底。

1. FP16 格式（IEEE 754 half precision）​

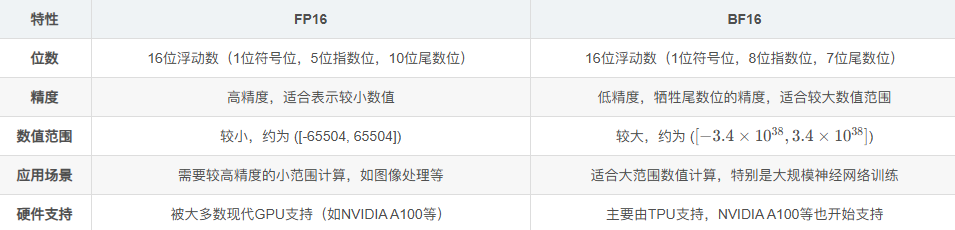
位数分布：

部分位数
符号位1
指数（Exponent）5
尾数（Mantissa）10

浮点数公式：

x=(−1)s⋅(1.m)2⋅2(e−bias) x = (-1)^s \cdot (1.m)_2 \cdot 2^{(e-bias)}

其中

bias=2k−1−1=24−1=15\text{bias} = 2^{k-1} - 1 = 2^4 - 1 = 15

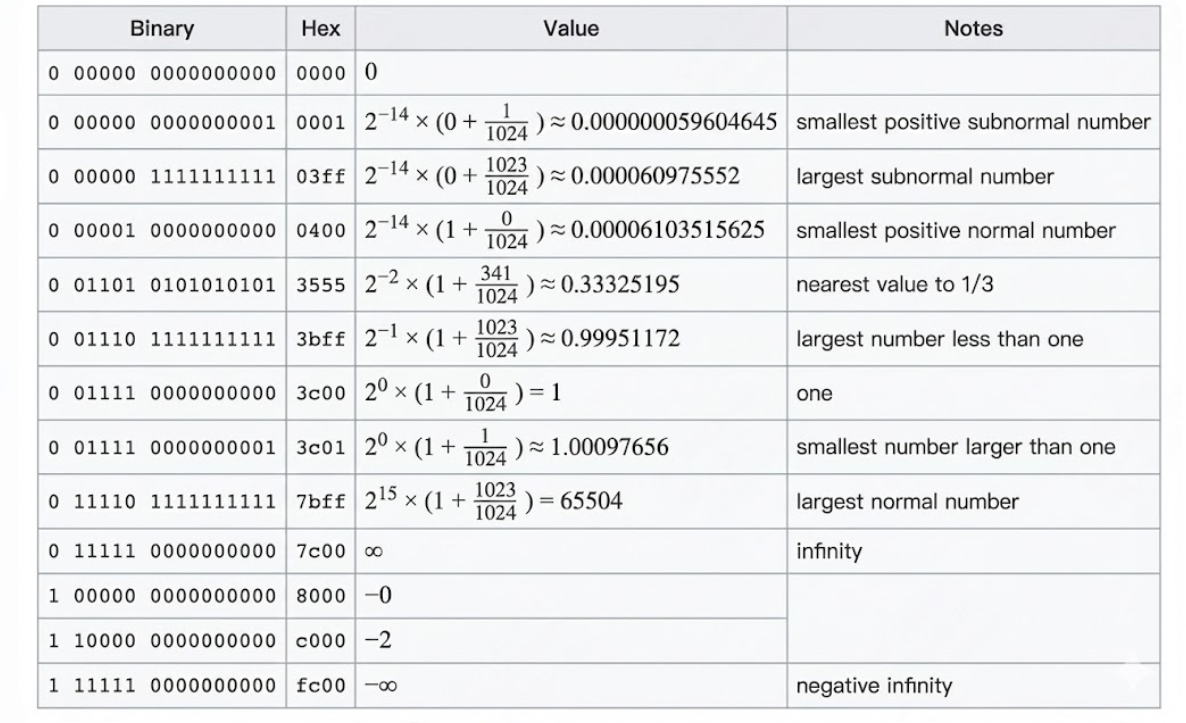
image-20251224194252889

FP16 最大值怎么算？​

指数最大值：

  • 指数 e 最大值 = ( 11110_2 = 30 )（保留最高值 31 用于 inf / nan）

所以：

actual exp=30−15=15\text{actual exp} = 30 - 15 = 15

尾数最大：(binary)

1.11111111112=1+(1−2−10)=1.9990234375 1.1111111111_2 = 1 + (1 - 2^{-10}) = 1.9990234375

最大值：

max=1.9990234375×215 \text{max} = 1.9990234375 \times 2^{15}

计算：

215=32768 2^{15} = 32768

所以：

max≈1.999×32768≈65504\text{max} \approx 1.999 \times 32768 \approx 65504

所以 FP16 范围约为：[-65504, 65504]

FP16 最小正值怎么算？​

指数最小正规：

e=1(binary 00001) e = 1 \quad(\text{binary }00001)

实际指数：

1−15=−14 1 - 15 = -14

尾数最小正规 = 1.0

min normal=1.0×2−14=116384≈6.1035×10−5 \text{min normal} = 1.0 \times 2^{-14} = \frac{1}{16384} \approx 6.1035 \times 10^{-5}

这也是 FP16 的标准数据。

BF16 的数值范围为什么特别大？​

BF16（Brain Floating Point）：

BF16 部分位数
符号1
指数8（与 FP32 一样）
尾数7

注意：BF16 的指数位数与 FP32 相同（都是 8 位）！

FP32 bias = 127 BF16 也沿用这一点。

BF16 最大值推导​

指数最大正规：

e=111111102=254 e = 11111110_2 = 254

实际指数：

254−127=127 254 - 127 = 127

尾数最大：

1.11111112=1+(1−2−7)=1.9921875 1.1111111_2 = 1 + (1 - 2^{-7}) = 1.9921875

最大值：

1.9921875⋅21271.9921875 \cdot 2^{127}

2ⁱ 转成十进制：

2127≈1.7014×1038 2^{127} \approx 1.7014 \times 10^{38}

最大值：

BF16max⁡≈3.4×1038 BF16_{\max} \approx 3.4 \times 10^{38}

和 FP32 的范围一样。

FP32​

​ fp32又被称为单精度浮点表示，是深度学习中标准的精度表示，由32bit组成(4bytes)，分为3个部分:

FP32 部分位数
符号1
指数8（与 BF16一样）
尾数23

总结​

  • 从占用存储角度看，fp16占据2 bytes，bf16占据2 bytes，fp32占据4 bytes
  • 从数值表达范围来看：fp32 = bf16 > fp16
  • 从数值表达精度来看：fp32 > fp16 > bf16
  • 深度学习训练中，一般采用fp32，但出于节省存储，加快训练的目的，我们也会采用混合精度训练，即fp32 + fp16/bf16，这块细节将在下文说明